こんにちは、IDEAの笠井です。

【ステップⅠ】では、線画を始めるにあたって、直線や円を描く練習をしていただきました。そして、身の周りの立体の多くは直線と楕円とで構成されていることをお伝えしました。

今回は、奥行きのある立体が自然に（正しく）見える線画の描き方のコツをお伝えします。理論に基づいた線画の基本であり、この先、楕円や回転体を描く際にも使いますから、しっかり理解していただきたいと思います。

理論を学んだ後で、立体の中でも最もイメージしやすく、形の正しさも確認しやすい立方体を、実際に描いてみましょう。

【ステップⅡ】－パース（透視図法）の基本－

立体を、見たままのように描くための理論をパース（Perspective：透視図法）といいます。

パースは、紙などの平面に立体物を表現する方法として、子供の頃に習ったことがある“遠近法”と同じものと考えていただいて構いません。“近くにあるものは大きく、遠くにあるものは小さく見える”というアレです。

試しに左右の手の人差し指を立てて、左腕は肘から曲げ、右腕は前方に伸ばして目の高さに合わせて見てください。右手の方が人差し指の長さが短く、手の大きさも小さく見えますね？

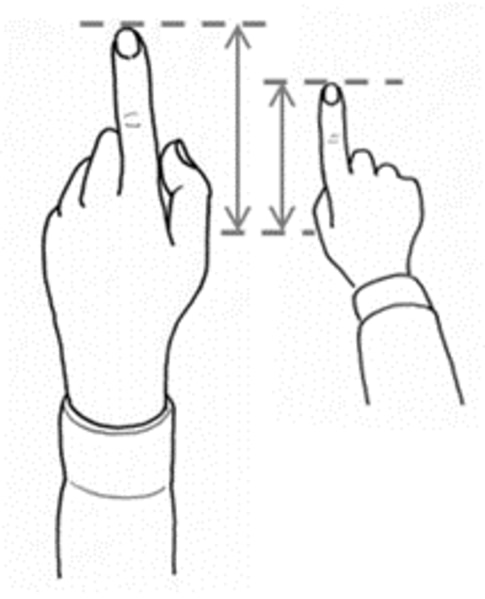
これからお伝えする立体の線画表現はすべてこのパースに則っていますから、しっかりと理解しましょう。

パースの特徴は以下の２点です。

1. 空間にある平行な線は、消失点（Vanishing Point）と呼ばれる一点に収束する
   
   
2. 奥行きは、正しい長さより縮んで（短く）作図される

言葉だけでは分かりにくいと思いますから、立体を描くときの基本である立方体（正六面体）を使って説明します。六つの面がすべて正方形でできている立方体は、作図したときに辺の長さがどう変化したかが分かりやすいという特徴があります。

パースで作図する透視図は以下の４種類に分類されます。

• １点透視図
• ２点透視図
• ３点透視図
•  等角投影図（アイソメトリック図）

① １点透視図 ：立方体の一つの面が、視点に正対している場合の見え方です。奥行きを示す辺だけが、水平線上の中心にある消失点（P）に収束して点を結びます。そのほかの縦の辺同士、横の辺同士は平行線になります。

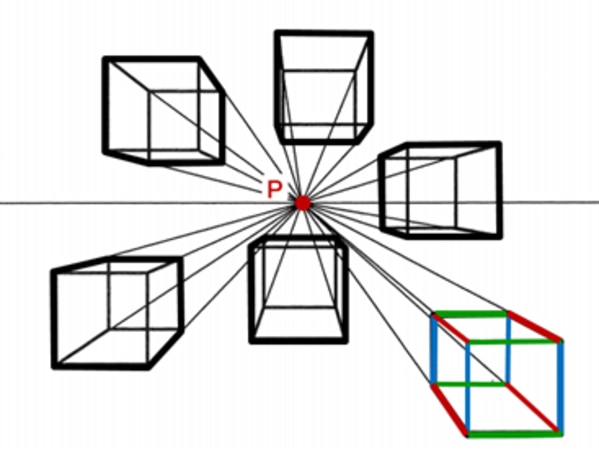
② ２点透視図 ：一つの縦の辺が視点に正対している場合の見え方で、その左右の辺が水平線上の二つの消失点（P1、P２）に収束します。高さを示す縦の辺は収束しないで平行線になります。

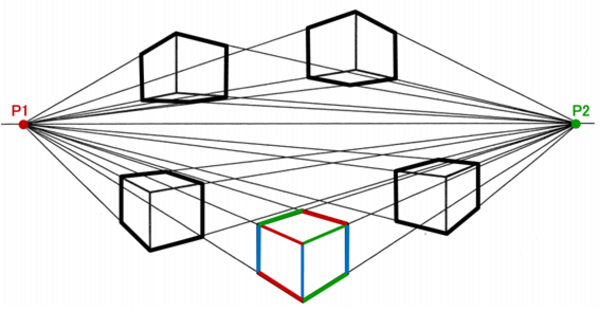
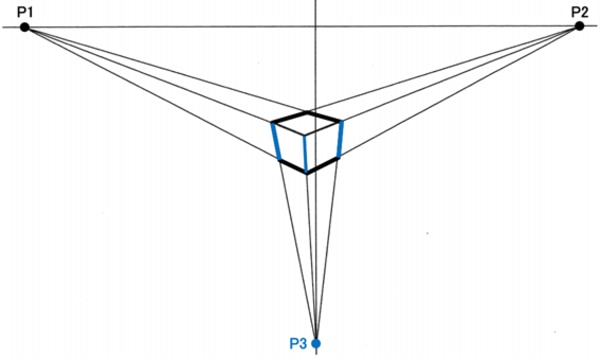
③ ３点透視図 ：２点透視図に垂直方向（上・下いずれか）の消失点（P３）が一つ加わったものです。縦の辺は消失点（P３）に収束し、立方体を忠実に再現できます。

• ※対象物の大きさに対して視点の位置が特に近い場合（ビルを真下から見上げたときなど）に適用します。多くの場合は、②の２点透視図で対応できます

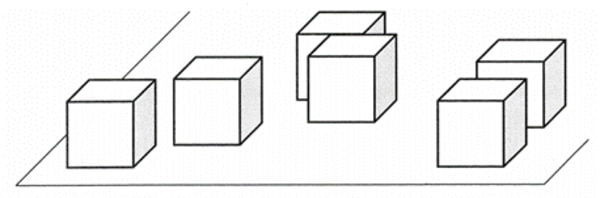
④ 等角投影図（アイソメトリック図）：望遠レンズで極端に遠くのものを見た場合に相当する表現で、透視図のような消失点は存在しません。立方体の向かい合う辺がすべて平行線として現れるため、複雑な要素のつながりや位置関係などの表現に適しています。

ただし、パースの特徴２項目「奥行きは正しい長さより縮んで（短く）作図される」に反していますから、末広がりのように見えてしまいます。

以上が、立体を自然に見えるように描くためのパースの基本です。ここから先の線画はすべてパースで描いていきますので、直線や円を描いたのと同じように、立体を描く練習をしてみましょう。

まずは、利用頻度の多い①１点透視図や②２点透視図の説明にならって、色々な大きさの立方体を、色々な角度から見たように描いてみてください。

そのとき消失点はぜひ意識してほしいのですが、閃いたアイデアを素早く描くのが目的ですから、厳密に考える必要はひとまずありません。思いのままに描いてみて、その線画をあとで見たときに立方体の面が捻じれていたり、辺が平行に見えなかったり、直交して見えなかったり、おかしいなと感じたら、その原因を考えてみてください。

下の図は、A4サイズの紙に消失点（P1、P2）を設定して、それを目安にフリーハンドで（定規を使わずに）立方体を描いたものです。少し慣れたら目安としての消失点も設定しないで描けるようになります。

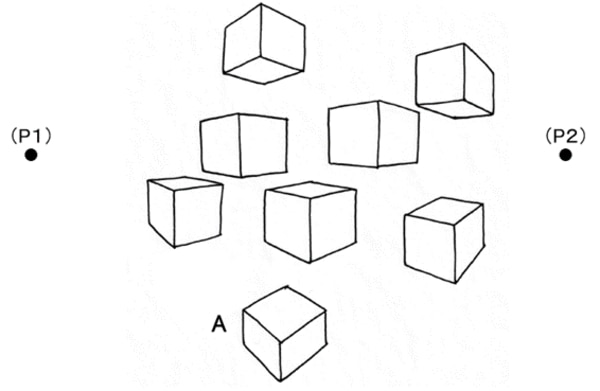
ここでちょっと説明を加えたいと思います。実は①１点透視図や②２点透視図で描く場合、立体が正しく（自然に）見えるのは、消失点の位置（高さ）よりも上下方向にあまり離れない範囲に限られているのです。その理由を以下に述べます。

上のA図をご覧ください。他の立方体と比べて手前の角が９０度に近くなっていますね？　

立方体が消失点から離れていない高さにあるときには手前の角はかなり鈍角ですが、下がるに従って手前の角は９０度（正方形の角）に近づきます。言い換えると、A図はかなり上から見下ろしている図といえるのです。それを下の図で説明しましょう。

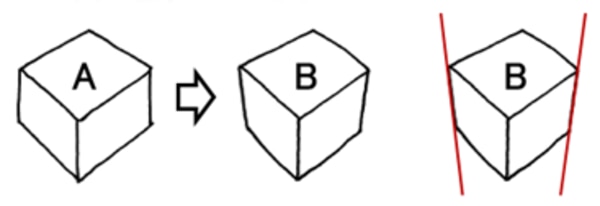
上のA図と同じものを下の左端に描き写してみました。上ではそれほどおかしく見えなかったと思いますが、その右側に描き足したB図と見比べてみてください。

いかがですか？　こうしてみると、B図の方が自然に見えませんか？

ですが、B図の上面と手前の縦の辺はA図と全く同じなのです。もうお分かりですね？　B図は、右端の図で示したように、③３点透視図にならって左右の縦の辺を傾けて描いています。このように、立体の位置によっては３点透視による補正が必要になることを知っておいてください。

いかがですか、立方体の描き方に慣れましたか？　次回は立方体の分割と倍増の方法、そしてそれを応用した直方体の描き方に進んでいきます。

さあ、複雑な立体の線画表現までもう少しです。

笠井＠IDEA